Konum Vektörü Konusu

“Konum Vektörü” terimi tipik olarak bilgisayar bilimlerinde, özellikle grafik ve uzamsal hesaplamalar alanında kullanılan matematiksel bir yapıyı ifade eder.Konum vektörü, çok boyutlu bir uzayda bir noktanın veya konumun temsilidir ve bilgisayar grafiklerinden coğrafi bilgi sistemlerine (CBS) kadar çeşitli uygulamalarda yaygın olarak kullanılmaktadır.Bu yazıda konum vektörü kavramını, önemini ve uygulamalarını inceleyeceğiz.

Konum Vektörlerini Anlama

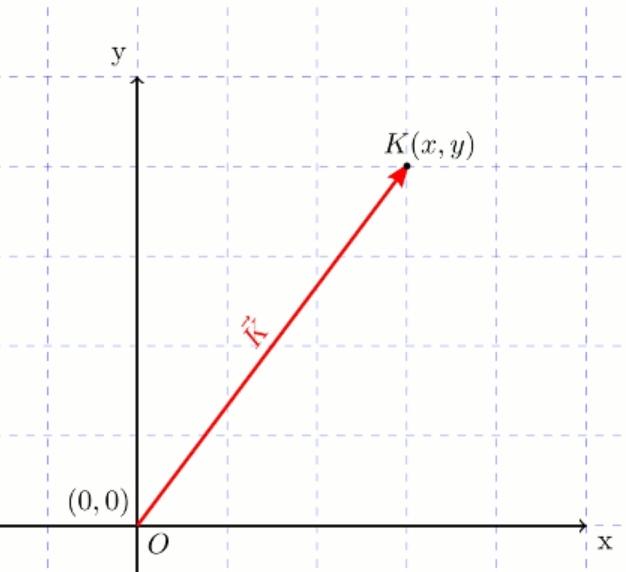
Bir konum vektörü, esasen uzaydaki bir konumun matematiksel bir temsilidir.Genellikle, her koordinatın uzaydaki bir boyuta karşılık geldiği sıralı bir koordinat kümesi olarak ifade edilir.İki boyutlu uzayda, bir konum vektörü (x, y) olarak temsil edilebilirken, üç boyutlu uzayda (x, y, z) ‘ye kadar uzanır.N boyutlu bir uzay için genel biçim(x₁, x₂, …, xₙ).

Örneğin, bir 2B uzayda, koordinatlarda (3, 4) bulunan bir noktamız varsa, karşılık gelen konum vektörü [3, 4] olacaktır.Bir 3B alanda, bir nokta (1, 2, 5) konumundaysa, ilişkili konum vektörü [1, 2, 5] olur.

Bilgisayar Grafiğindeki Önemi

Konum vektörleri bilgisayar grafiklerinde çok önemli bir rol oynar.Grafiksel uygulamalarda nesneler sanal bir alanda konumlandırılır, manipüle edilir ve işlenir.Konum vektörleri, bu alandaki nesnelerin veya noktaların konumunu tanımlamaya yardımcı olur.

Bir sahneyi oluştururken, bilgisayar grafik sistemleri nesnelerin ekrana nereye yerleştirilmesi gerektiğini belirlemek için konum vektörlerini kullanır.Bu vektörlerin dönüşümleri ve manipülasyonları yoluyla ölçekleme, döndürme ve çeviri gibi çeşitli etkiler elde edilebilir.Örneğin, bir nesneyi farklı bir konuma çevirmek, konum vektörünü buna göre değiştirmeyi içerir.

Coğrafi Bilgi Sistemlerinde (CBS) Uygulamalar

Coğrafi verilerin analizi ve görselleştirilmesi ile ilgilenen Coğrafi Bilgi Sistemlerinde konum vektörleri esastır.CBS uygulamaları genellikle belirli coğrafi konumlara bağlı verileri yönetmeyi ve analiz etmeyi içerir.Konum vektörleri, Dünya yüzeyindeki bu noktaları temsil ederek hassas haritalama ve mekansal analize olanak tanır.

Örneğin, bir CBS, çeşitli yer işaretlerinin, şehirlerin veya çevresel özelliklerin koordinatlarını temsil etmek için konum vektörlerini kullanabilir.Bu vektörler arasındaki ilişkileri analiz etmek, kalıplar, eğilimler ve mekansal korelasyonlar hakkında fikir verebilir.

Matematik ve İşlemler

Konum vektörleri çeşitli matematiksel işlemlere tabidir.İki nokta arasındaki mesafe, açı hesaplamaları ve dönüşümler, konum vektörlerinin manipüle edilmesini içerir. LÖrneğin, bir uzaydaki iki nokta arasındaki Öklid mesafesi, ilgili konum vektörlerinin koordinatları kullanılarak belirlenebilir.

Sonuç olarak, konum vektörü bilgisayar bilimlerinde, özellikle bilgisayar grafikleri ve CBS’DE temel bir kavramdır.Çok boyutlu uzayda noktaları temsil etme yeteneği, onu çok çeşitli uygulamalar için çok yönlü bir araç haline getirir.Gerçekçi grafikler oluşturmak veya coğrafi verileri analiz etmek olsun, konum vektörlerinin kullanımı, uzaydaki konumları doğru bir şekilde temsil etmek ve manipüle etmek için çok önemlidir.Teknoloji ilerlemeye devam ettikçe, konum vektörlerinin rolünün daha da genişlemesi ve grafik ve CBS’NİN ötesindeki alanları etkilemesi muhtemeldir.